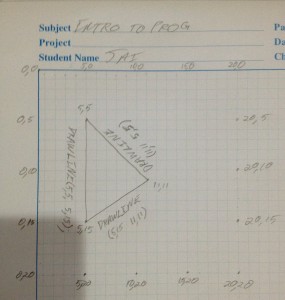
This picture shows a small grid of “pixels”, 20×20 large.

If you count the pixels along the top, you’ll see that I’ve marked off every 5 pixels, just for clarity. That’s the X axis, moving from 0 at the left to 20 at the right.

On the side, we have the Y axis, moving from 0 at the top to 20 at the bottom. Computer graphics traditionally start with 0 at the top, but other fields such as CAD or robotics often have 0 at the bottom for Y, and 20 (or whatever) at the top. Not important at the moment, we’ll work with 0Y at the top.

So every pixel inside the grid can be thought of as a point in that grid. If you count along 7 pixels, the X value will be 7, and then if you count down 12, the Y value will be 12. That’s always expressed as (X, Y) – the sideways direction first. That’s to annoy mathematicians who use matrices that express the row first, then the column 🙂

Inside the grid, then, I’ve drawn 3 lines. Start at the top left – you can see a point labelled (5,5). If we draw a line straight down, we’re adding to the Y value but not moving sideways, so the X is unchanged. I’ve drawn down 10 pixels, so the final value is (5,15). Similarly, I can start at (5,15) and move both up *and* sideways. Moving 6 to the right gives me 5+6 for X, moving up (towards 0) 4 gives me 15-4 for Y, so (11,11). And a final line again moves in both directions back to the start.

So each line has a start position (5,5) and an end position (5, 15), because a line has a start point and end point:

(5,5) (5,15)
(5,15) (11,11)
(11,11) (5,5)

Shapes like triangles and squares are just lines, but they’re lines with a special quality – each line shares a point with another line. They *have* to join up. So if our first line is (5,5) to (5,15), we don’t need to specifiy (5,15) for the second line – it has to start at (5,15). If it ends at (11,11), then we know the start for the next line. And you can see from the list above that there are indeed 3 unique point – (5,5), (5, 15) and (11,11).

So although at some level we have to draw each line between two points, we can get away with only providing the points if they are shared. If we say “Draw a triangle between (5,5), (5,15) and (11,11)”, we can just “join the dots” as it were.

Hope that helps!